# Array Rotation In-Place
- Suppose we are given an array of n integers and we have to rotate it by k positions to the left with space complexity of O(1) i.e. within the same array (in-place).
If we will shift elements one by one it will become hard to keep tack of all elements without using additional space.
So we will divide the array into sets/cycles where the number of sets will depend on the value of n and k.
Number of sets = gcd( n, k )where gcd is greatest common divisor of n & k.And we will shift every element in a set k places to the left by using the formula
A[j] = A[ ( j + k ) % n]So there will be two nested loops where the outer loop will run for the number of sets and the inner loop with shift elements of a set k positions to the left.
Let outer loop be from
i=0 to i < gcd(n,k)i.e for the number of sets.Inside the inner loop we will shift the elements k positions to the left for each set i.e starting for i=0.
- We will take a variable
jfor the inner loop and makej = i - We will copy the value of first element of the set in a temporary varivale "temp"
- Then we will calculate
d = (j + k) % n - And make
A[j] = A[d] - Then we will move j to the index of the shifted element by making
j = d - And we will repeat the steps 2 to 5 until
j == i, i.e. whenj == iwe will break out of the inner loop.
- We will take a variable
After the inner loop ends we will copy the value in temp at index
ji.eA[j] = tempAnd we will repeat the steps for every set.
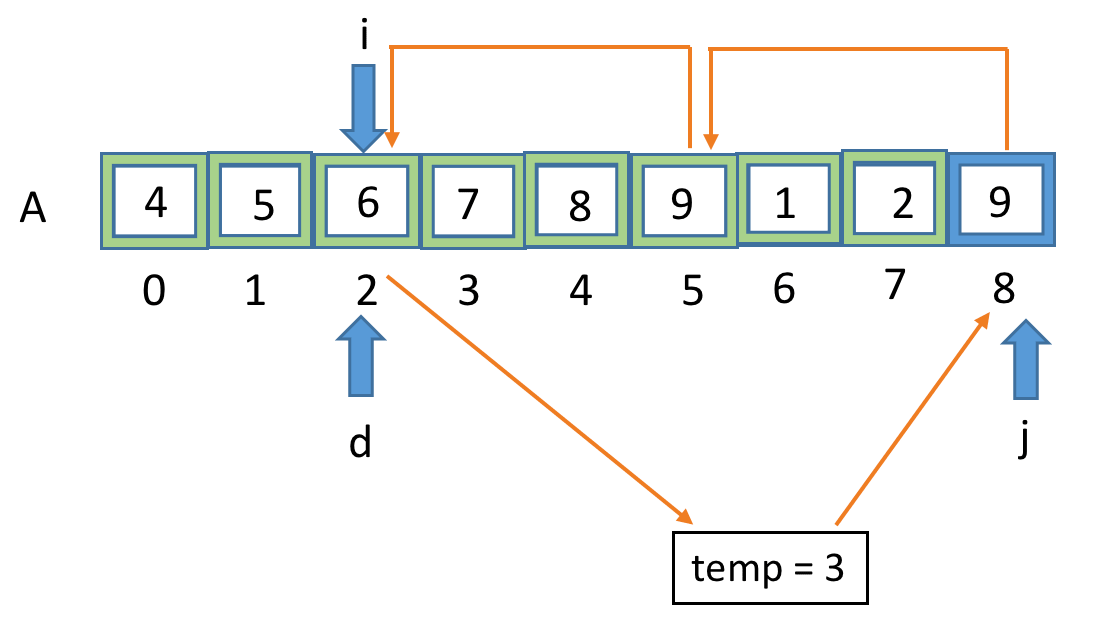
Suppose we are given this array of 9 elements i.e n=9 and we have to rotate it by 3 positions i.e. k=3.
- Then gcd of 9 & 3 will be 3, therefore we will divide this array into 3 sets and perform shift operation on elements of each set as follows:

# Source Code - C++
#include <iostream>
using namespace std;
int gcd(int a, int b)
{
if(b==0)
return a;
else
return gcd(b, a%b);
}
void ArrayRotate (int A[], int n, int k)
{
int d=-1,i,temp,j;
for(i=0;i<gcd(n,k);i++)
{
j=i;
temp=A[i];
while(1)
{
d=(j+k)%n;
if(d==i)
break;
A[j]=A[d];
j=d;
}
A[j]=temp;
}
}
void displayArray(int A[],int n)
{
int i;
for(i=0;i<n;i++)
cout<<A[i]<<" ";
cout<<"\n";
}
int main()
{
int n,i,k;
cout<<"Enter size of the Array\n";
cin>>n;
int A[n];
cout<<"Enter Array elements\n";
for(i=0;i<n;i++)
cin>>A[i];
cout<<"Enter the value of k\n";
cin>>k;
displayArray(A,n);
ArrayRotate(A,n,k);
displayArray(A,n);
return 0;
}
Time Complexity : O(n)
Space Complexity : O(1)



